Уравнение Шредингера

Обнаружение волновых свойств микрочастиц ') свидетельствовало о том, что классическая механика ие может дать правильного описания поведения подобных частиц. Возникла необходимость создать механику микрочастиц, которая учитывала бы также и их волновые свойства. Новая механика, созданная Шредингером, Гайзен-бергом, Дираком и другими, получила название волновой или квантовой механики.

Основным уравнением квантовой механики является уравнение Шредингера. Подобно тому, как уравнения динамики Ньютона ие могут быть получены теоретически, а представляют собой обобщение большого числа опытных фактов, уравнение Шредингера также нельзя

310

вывести из каких-либо известных ранее соотношений. Его следует рассматривать как исходное основное" предположение, справедливость которого доказывается тем обстоятельством, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.

Состояние микрочастицы описывается в квантовой механике так называемой волновой функцией, которую принято обозначать буквой *¥. Она является функцией координат и времени и может быть найдена путем решения уравнения:

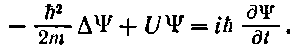
Это уравнение было установлено Шредингером в 1926 г. и называется уравнением Шредингера со временем (или временным уравнением Шредингера). Величины, входящие в это уравнение, имеют следующие значения: /—мнимая еди ми ца;

fi — постоянная Планка, деленная на 2л; т — масса частицы;

А-оператор Лапласа \^дч' = ^ + —- + —J;-

U — потенциальная энергия частицы.

Как следует из уравнения (65.1), вид волновой функции ^w определяется потенциальной энергией U, т. е., в конечном счете, характером тех сил, которые действуют па частицу. Вообще говоря, U есть функция координат и времени. Для стационарного (не меняющеюся со временем) силового поля U не зависит явно от времени. В последнем случае волновая функция ^w распадается на два множителя, один из которых зависит только от времени, второй — только от координат:

Ч(х, у, 2, t) = e-*w»*${x, y_} z)           (65.2)

(Е — полная энергия частицы).

В самом деле, подстановка функции (65.2) в уравнение (65.1) дает:

- -|L Дфе-* дао * ₊ щ_е-1 №/*) *= /й (- * -у) фе~* ^{Elh)i-

Сокращая все члены этого уравнения на общий множитель e~^lKElh) и произведя соответствующие преобразова-

(65.1)

ния, получим Дифференциальное уравнение, определяющее функцию \|?:

Если функция U зависит от времени явно, то и решение последнего уравнения — функция tf — будет зависеть от времени, что противоречит предположению (65.2),

Уравнение (65.3) называется уравнением Шре-дингера для стационарных состояний (пли уравнением Шредингера без времени). В дальнейшем мы будем называть его просто уравнением Шредингера.

К уравнению Шредингера можно прийти путем следующих рассуждений. Из опытов по дифракции микрочастиц вытекает/ что параллельный пучок частиц обладает свойствами плоской волны, распространяющейся о направлении движения частиц. Уравнение плоской волны, распространяющейся в напраплешш осп x_f имеет, как известно, вид:

(65.3)

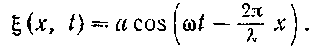
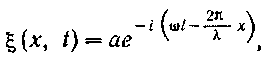
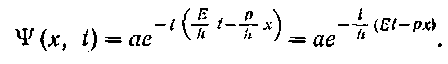
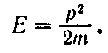
Это выражение часто пишут в комплексном виде:

подразумевая, что надо принимать во внимание вещественную часть этого выражения [см. т. I, формулу (79,9)].

Согласно гипотезе де-Бройля свободному движению частицы соответствует плоская волна с частотой м ~ = E/ft и длиной волны К = 2пЬ/р. Заменяя йий выражении (65.4) энергией и импульсом частицы, получим волновую функцию для свободной частицы, движущейся в направлении оси х:

(65.4)

(65.5)

Чтобы найти дифференциальное уравнение, которому удовлетворяет функция (65.5), воспользуемся соотношением между Е и р:

(65.6)

Продифференцировав функцию (65.5) один раз по t_r а второй раз дважды по х, получим:

Из этих соотношений можно выразить Е и р² через функцию У и ее производные:

Подставляя последние выражения в соотношение (65.6), получим дифференциальное уравнение;

Если направление волны не совпадает с осью х (или у, или г) у фаза колебаний будет зависеть от всех координат: х, у и z. Можно показать, что в этом случае дифференциальное уравнение имеет вид:

Полученное уравнение совпадает с уравнением Шре-дингера (65.1) для случая U^O (частица по условию свободна). Подстановка (65.2) б это уравнение (такая подстановка правомерна, так как О = 0, т. е. не зависит от t) приводит к уравнению Шредипгера для стационарных состояний:

Это уравнение совпадает с уравнением (65.3) для случая £/ = 0.

Таким образом, мы получили уравнение Шредипгера для свободно движущейся частицы. Теперь следует обобщить уравнение (65.7) на случай частицы, движущейся в потенциальном поле сил, когда полная энергия Е слагается из кинетической энергии Т и потенциальной энергии U,

(65.7)

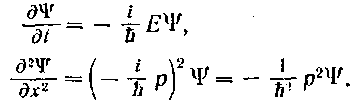
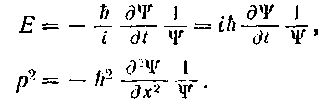
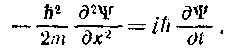
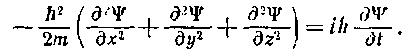
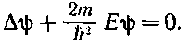
В случае свободной частицы полная энергия Е совпадает с кинетической 7\_гтак что величину Е в уравнении (65.7) можно трактовать либо как полную, либо как кинетическую энергию частицы. Обобщая уравнение (65.7) на случай движения частицы в поле сил, нужно решить вопрос о том, что следует подразумевать для такой частицы под величиной Е: полную или только кинетическую энергию. Если принять, что £ —полная энергия частицы, обобщенное уравнение, определяющее t|?, а значит, и сама ^ не будет зависеть от вида функции (У, т. е. от характера силового поля. Это, очевидно, не может соответствовать действительному положению вещей. Поэтому следует признать, что при наличии сил, действующих на частицу, вместо Е в уравнение (65.7) нужно Евести кинетическую энергию частицы Т—Е—U. Произведя такую замену, мы придем к уравнению (65.3).

Чтобы предостеречь читателя от иногда встречающегося заблуждения, необходимо еще раз подчеркнуть, что приведенные нами рассуждения не могут рассматриваться как вывод уравнения Шредингера. Их цель — пояснить, каким образом можно было прийти к установлению вида волнового уравнения для микрочастицы. Доказательством же правильности уравнения Шредингера может служить лишь согласие с опытом тех результатов, которые получаются с помощью этого уравнения.