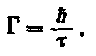Ширина спектральных линий

Из возбужденного состояния атом может перейти спонтанно (самопроизвольно) в более низкое энергетическое состояние. Время, за которое число атомов, находящихся в данном возбужденном состоянии, уменьшается в е раз, называется временем жизни возбужденного состояния¹). Время жизни возбужденных состояний атомов имеет порядок 10~⁸—10~⁹ сек. Время жизни метастабильных состояний может достигать десятых долей секунды.

Возможность спонтанных переходов указывает на то, что возбужденные состояния нельзя рассматривать как строго стационарные. В соответствии с этим энергия возбужденного состояния не является точно определенной и возбужденный энергетический уровень имеет

конечную ширину. В квантовой механике доказывается, что ширина уровня обратно пропорциональна времени жизни т возбужденного состояния:

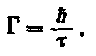(79.1)

Основное состояние атома стационарно (из него невозможен спонтанный переход в другие состояния). Поэтому энергия основного состояния является определен* ной вполне точно.

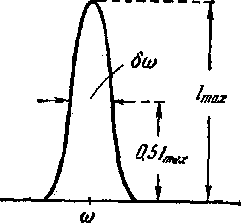
Вследствие конечной ширины возбужденных уровней энергия испускаемых атомами фотонов имеет разброс, описываемый кривой, изображенной на рис. 222. Соответственно спектральная линия обладает конечной шириной ¹):

Взяв т ~ 10~⁸ сек, получим для бшо значение порядка 10⁸ сек-¹. Интервал частот б(о связан, с интервалом длин волн Ь% соотношением:

(79.3)

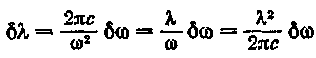
(знак минус мы опустили).

Выражения (79.2) и (79.3) дают так называемую естественную ширину спектральной линии. Подставив в (79.3) — 5000 А и ~ 10⁸ сек-\ получим для естественной ширины спектральной линии значение порядка Ю^-4 А.

Тепловое движение излучающих атомов приводит к дополнительному так называемому допплеровско-

му расширению спектральные линий. Пусть в мо* мент испускания фотона атом обладает импульсом р₀ и соответственно энергией поступательного движения

(т_а — масса атома). Фотон уносит с собой импульс fik, равный по модулю Ьы/с [см. (57.5)]. Поэтому цмпульс атома изменяется и становится равным

. Следовательно, изменяется и энергия поступательного движения атома. Обозначим через A£w изменение внутренней энергии атома, т. е. разность

, где—значения энергии уровней, меж-

ду которыми совершается переход. На основании закона сохранения энергии должно равняться сумме энер-

гии фотона и изменения энергии поступательного Движения излучающего атома:

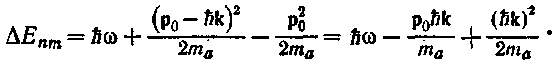
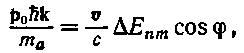
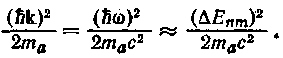
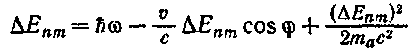
Изменение энергии поступательного движения атома мало по сравнению с энергией фотона Ью. Поэтому в первом приближении можно считать, что, как мы и поступали в предыдущих параграфах. Заменив hk через и учтя, что (v — скорость теплового движения атома), слагаемое в формуле (79.4) можно представить в виде:

где ф — угол между ро и fik, который может изменяться в пределах от 0 до л. В том же приближении

Таким образом, формуле (79.4) можно придать вид:

Найдем среднее значение энергии отдачи, приобретаемой атомом при испускании фотона. В отдельном акте излучения атом получает, энергию;

Согласно (79.6) эта величина равна

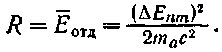
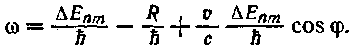
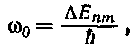
В источнике излучения, в котором все направления теплового движения атомов равновероятны, cos<p принимает все значения от —1 до +1. Следовательно, частоты излучающих фотонов будут заключены в пределах интервала бес д. Таким образом, выражение (79.10) дает допплеровскую ширину спектральной линии. Из (79.10)

Среднее значение этого выражения равно первому слагаемому (cos ф принимает ■ с равной вероятностью все значения от —1 до 4-1, вследствие чего второе слагаемое в среднем равно нулю).

Итак, обозначив среднюю энергию отдачи, приобретаемую атомом при испускании фотона, буквой R, можно написать:

С учетом (79.7) формулу (79.6) можно записать следующим образом:

Разрешив это уравнение относительно частоты фотона ш, получим:

Наконец, введя обозначения:

мы придем к соотношению:

следует, что относительное допплеровское уширение линий бос/о не зависит от частоты и равно 2(v/c). Согласно (79.3) . Средняя скорость атомов (с атомным весом ~ 100) при температуре порядка нескольких тысяч градусов составляет приблизительно 10³ м)сек. В этих условиях допплеровская ширина спектральной линии для К = 5000 А будет равна

Действительная ширина спектральной линии слагается из естественной ширины (79,2) и допплеровской ширины (79.10):

Середина линии приходится на частоту [см. (79.11)]. Величина со₀ представляет собой ту частоту, которую имел бы фотон при условии, что энергия Д£пт полностью пошла на излучение. Получение атомом при излучении энергии отдачи R привадит к смещению спектральной линии в сторону меньших частот (т. е. больших длин волн) на величину , определяемую

формулой (79.9). Заменив в этой формуле R согласно (79.7), получим:

Из этого выражения следует, что относительное смещение частоты оказывается пропорциональным частоте.

Оценим Дсоя для видимого света (со ~ 3-Ю¹⁵ се/с*^-1). Массу атома положим равной 10~²² г (атомный вес порядка 100). По формуле (79.12)

откуда для получается значение порядка 10~⁷ А, ко-

торым вполне можно пренебречь.

Заметим, что при поглощении атомом фотона Ьш импульс фотонасообщается атому, вследствие чего атом приходит в поступательное движение. Энергия этого движения может быть определена по формуле (79.7).

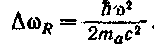
Следовательно, для того чтобы вызвать в атоме переход , фотон должен обладать энергией:

а частота фотона должна быть равна Гдеопределяется формулой (79.9).

Таким образом, спектральная линия, середина которой лежит в спектре испускания данного атома при частоте , в спектре поглощения того же атома

будет иметь частоту . Для видимого света

смещение линий испускания и поглощения друг относительно друга (составляющее) на пять порядков меньше допплеровской ширины линии (равной ~3'10~²А) и на три порядка меньше естественной ширины линии (равной ~ 10~⁴ А). Следовательно, для видимого света линии испускания и поглощения можно считать точно совмещенными друг с другом.