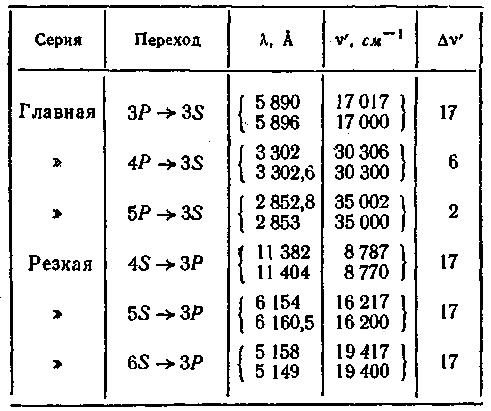
Исследование спектров щелочных металлов при помощи приборов с большой разрешающей силой показало, что каждая линия этих спектров является двойной (дублет). Так, например, характерная для натрия желтая линия состоит из двух линий с длинами волн 5890 А и 5896 А. То же относится и к другим линиям главной серии, а также к линиям других серий. В табл. 4 приведены некоторые дублеты натрия. В четвертом столбце указаны волновые числа линий v' [см. (59.2)]. В последнем столбце дано расщепление компонент дублетов (разность волновых чисел).

Расщепление спектральных линий, очевидно, обусловлено расщеплением энергетических уровней. Поскольку расщепление линий главной серии различно,а для линий резкой серии одно и то же(см. табл.), приходится предположить, что уровни S являются одиночными (синглетами), а уровни Р — двойными (дублетными) (см. рис. 204). Дальнейший анализ спектра натрия показал, что уровни D и F также являются двойными.

Структура спектра, отражающая расщепление линий на компоненты, называется тонкой структурой. Сложные линии, состоящие из нескольких компонент, получили название мультиплетов. Тонкая структура обнаруживается, кроме щелочных металлов, также и у других элементов, причем число компонент в муль-типлете может быть равно двум (дублеты), трем (триплеты), четырем (квартеты), пяти (квинтеты) и т. д. В частном случае спектральные линии даже с учетом тонкой структуры могут быть одиночными (синглеты).

Для объяснения мультиплетной структуры спектров и аномального эффекта Зеемана (см. § 75) Гаудсмит и Юленбек выдвинули в 1925 г. гипотезу о том, что электрон обладает собственным моментом импульса M_s, не связанным с движением электрона в пространстве. Этот собственный момент был назван спином.

Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Согласно этим представлениям электрон уподоблялся волчку или ве-

ретену. Кстати, отсюда происходит и сам термин «спин»: по-английски spin означает «верчение». Однако очень скоро пришлось отказаться от подобных модельных представлений, в частности по следующей причине. Вращающийся заряженный шарик должен обладать магнитным моментом, причем отношение магнитного момента к механическому должно иметь значение [см. (71.1)]:

(72.1)

Действительно, было установлено, что электрон, наряду с собственным механическим моментом, обладает также и собственным магнитным моментом \i₈. Однако ряд опытных фактов, в частности аномальный эффект Зеемана, -свидетельствует о том, что отношение собственных магнитного и механического моментов в два раза больше, чем для орбитальных моментов:

(72.2)

Таким образом, представление об электроне как о вращающемся шарике оказалось несостоятельным. Спин следует считать внутренним свойством, присущим электрону подобно тому, как ему присущи заряд и масса.

Предположение о спине электрона было Подтверждено большим количеством опытных фактов и должно, считаться совершенно доказанным. Оказалось также, что наличие спина и все его свойства автоматически вытекают из установленного Дираком уравнения квантовой механики, удовлетворяющего требованиям теории относительности. Таким образом, выяснилось, что спин электрона является свойством одновременно квантовым и релятивистским. В настоящее время также установлено, что спином обладают и другие элементарные частицы: протоны, нейтроны, фотоны и др.

Величина собственного момента импульса электрона определяется по общим законам квантовой механики [см. формулу (69.4)] так называемым спиновым квантовым числом s_? равным Vs¹);

(минус получается, если , плюс — если m_s = -V₂).

В ряд формул, в частности в выражение для энергии, входят не сами моменты, а их проекции. Поэтому принято говорить, что собственный механический момент (спин) электрона равен половине (подразумевается в единицах fi), а собственный магнитный момент равен одному магнетону Бора.

Рассмотрим теперь на примере атома натрия, как существование спина электрона может объяснить муль-типлетную структуру спектра. Поскольку момент атомного остатка равен нулю, момент атома натрия равен моменту оптического электрона. Момент же электрона будет слагаться из двух моментов: орбитального M_if обусловленного движением электрона в атоме, и спинового M_St не связанного с движением электрона в прастранстве. Результирующая этих двух моментов дает полный момент импульса оптического электрона. Сложение орбитального и спинового моментов в полный момент осуществляется по тем же квантовым законам, по которым складываются орбитальные моменты разных электронов [см. (70.2)]. Величина полного момента Доопределяется квантовым числом /;

Составляющая механического момента по заданному направлению может принимать квантованные значения, отличающиеся друг от друга на Ь:

(72.4)

Чтобы найти величину собственного магнитного момента электрона, умножим M_s на отношение (72,2) \i_sк M_s:

Знак минус указывает на то, что механический М₃и магнитный |i₃ моменты электрона направлены в противоположные стороны.

Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения:

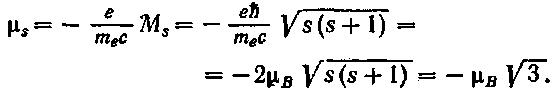(72.5)

(72.6)

причем / может иметь значения:

где / и s соответственно азимутальное и спиновое квантовые числа. При 1 = 0 квантовое число / имеет только одно значение:. При /, отличном от нуля, воз-

можны два значения: и , которые

соответствуют двум возможным взаимным ориентациям моментов Mi и M_s — «параллельной» и «антипараллель-ной» ¹).

Теперь учтем, что с механическими моментами связаны магнитные моменты, которые взаимодействуют друг с другом подобно тому, как взаимодействуют два тока или две магнитные стрелки. Энергия этого взаимодействия (называемого спин-орбитальным взаимодействием) зависит от взаимной ориентации орбитального и собственного моментов. Следовательно, состояния с различными / должны обладать различной энергией.

Таким образом, каждый терм ряда Р (/=1) расщепляется на два, соответствующих и ; каждый терм ряда D (1 = 2) расщепляется' на термы си, и т. д. Каждому терму ряда S (/ =-0) соответствует только одно значение; поэтому термы ряда S не расщепляются.

Итак, каждый ряд термов, кроме 5, распадается на два ряда — структура термов оказывается дублетной (двойной). Термы принято обозначать символами:

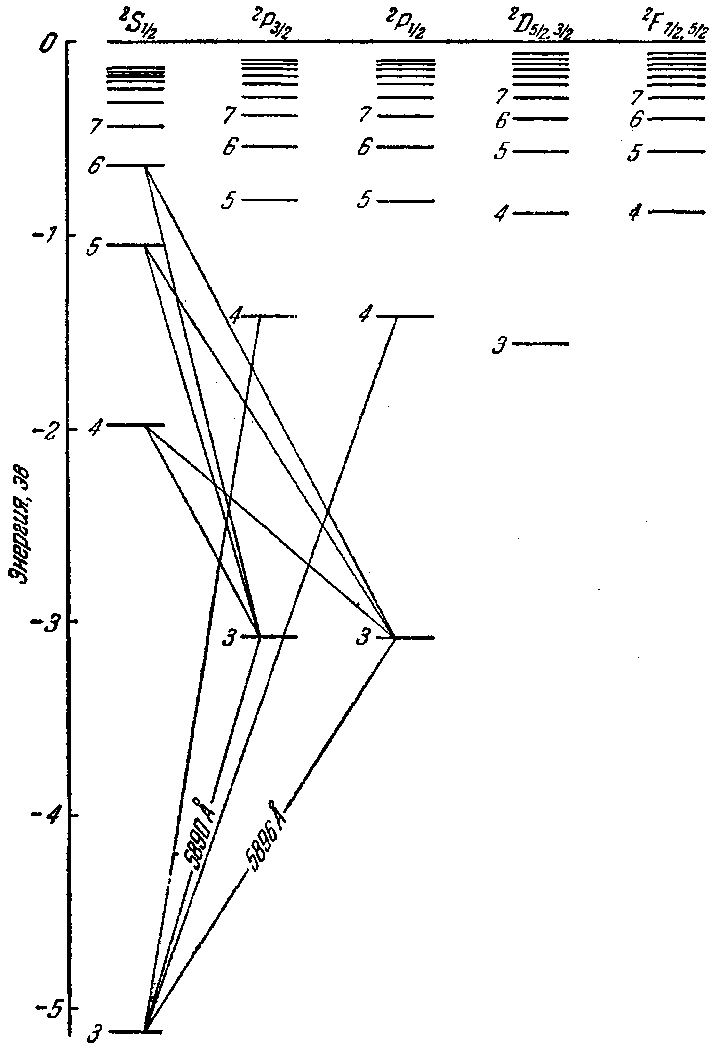
Рис. 204.

Правый нижний индекс дает значение /. Верхний левый индекс указывает мультиплетность термов. Хотя ряд 5 является одиночным, при символе терма ставится также 2, чтобы показать, что этот ряд принадлежит к системе термов, в целом дублетной.

С учетом тонкой структуры схема термов выглядит более сложно, о чем дают представление схемы уровней натрия (рис. 204) и цезия (рис. 205). Схему для натрия следует сравнить со схемой, изображенной на рис. 200. Поскольку мультиплетное расщепление термов D и F для натрия очень мало, подуровни D и F, отличающиеся значениями /, изображены на схеме слитно. Мультиплетное

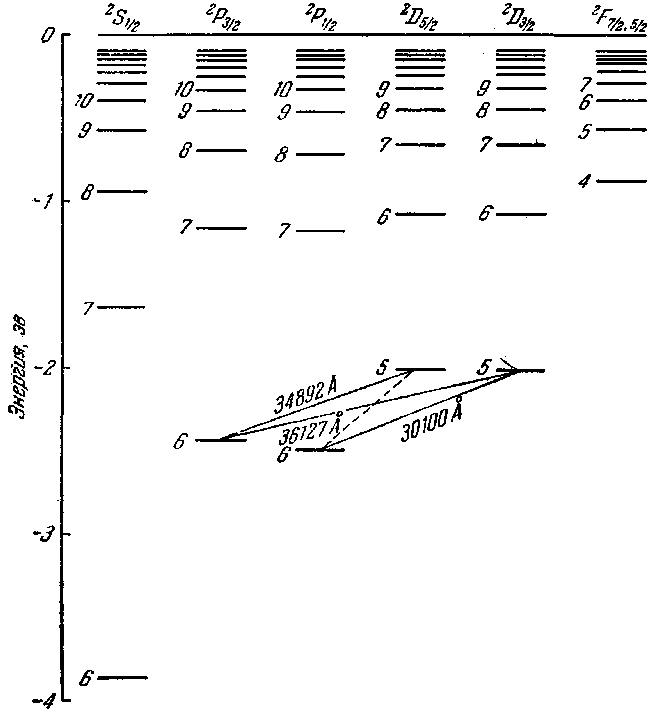
Рис. 205.

расщепление у цезия значительно больше, чем у натрия. На схеме цезия видно, что тонкая структура диффузной серии состоит не из двух линий, а из трех:

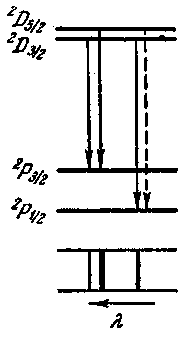
Возникновение этих линий пояснено дополнительно на рис. 206, Изображенный пунктиром переход

запрещен правилом отбора;

В нижней части схемы на рис. 206 показано, как выглядит сам мульти-плет. Толщина линий на^ схеме примерно соответствует" интенсивности спектральных линий. Совокупность получающихся линий выглядит как дублет, у которого одна из компонент в свою очередь оказывается двойной. Такая группа линий называется не триплетом, а сложным дублетом, так как она возникает в результате комбинации дублетных термов.

��.206

Заметим в заключение, что в связи с существованием спина электрона естественно возникает вопрос о том, что и у водородного атома уровни далжны быть двойными, а спектральные линии — дублетными. Тонкая структура водородного спектра действительно была обнаружена экспериментально.