Спектры щелочных металлов

Спектры испускания атомов щелочных металлов, подобно спектру водорода, состоят из нескольких серий линий. Наиболее интенсивные из них получили названия: главная, резкая, диффузная и основная (или серия Бергмана). Эти названия имеют следующее происхождение. Главная серия названа так потому, что наблюдается и при поглощении. Следовательно, она соответствует переходам атома в основное состояние. Резкая и диффузная серии состоят соответственно из резких и размытых (диффузных) линий. Серия Бергмана была названа основной (фундаментальной) за свое сходство с сериями водорода.

Еще 'в конце прошлого столетия Ридберг установил эмпирические формулы, позволяющие вычислить частоты серий щелочных металлов. Эти формулы для всех серий сходны и имеют вид:

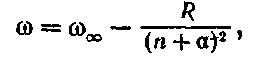
где—частота, соответствующая границе серии,— постоянная Ридберга (59,5),—целое число,—дробное число.

Таким образом, частоты линий могут быть представлены как разности двух термов: постоянного () и переменного, имеющего более сложный вид, чем баль-меровский терм. Константыи а для различных

серий имеют, вообще говоря, разное значение. Так, например, спектральные серии натрия можно представить следующими формулами.

Резкая серия(буква s является начальной буквой наименования серии: sharp — резкий).

Главная серия:(principal — главный),

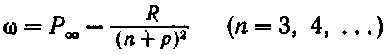
Диффузная серия:(diffuse — диффузный).

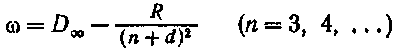
Основная серия (серия Бергмана)(fundamental — основной).:

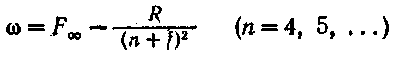
Вследствие равенства константы / нулю переменный терм в формуле для основной серии совпадает с баль-меровским, а сама серия, как уже отмечалось, является водородоподобной.

Для сокращения условились записывать переменные термы, указывая число п с добавлением букв S, P, D, F соответственно для каждой серии. Тогда переменный терм резкой серии вместобудет иметь вид/zS.

Переменный терм главной серии запишется как пР₉ диффузной — nD и, наконец, основной — nF.

Переписывая формулы для серий натрия с использованием сокращенных обозначений, учтем также то обстоятельство, что, как было установлено экспериментально, постоянный терм главной серии Р^ оказался совпадающим с переменным термом резкой серии для п = 3 (Роо = 35). Постоянные термы £<» и /)<*> оказались одинаковыми и равными переменному терму главной серии для п = 3 (Soo — Dm = ЗР). Постоянный терм основной серии Foo оказался равным переменному терму диффузной серии для п = 3 {Foo — 3D). Таким образом, спектральные серии натрия могут быть представлены в следующем виде:

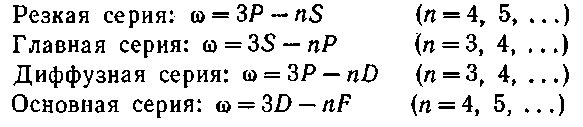
Мы пришли к весьма существенному результату. Выяснилось, что линии всех четырех спектральных серий можно получить путем комбинации четырех типов (рядов) термов: [ср. с формулой (59.9)].

Терм с точностью до постоянного множителя совпадает с энергией соответствующего состояния атома [см. формулу (62.2)]. Следовательно, каждому ряду спектральных термов должен соответствовать свой ряд энергетических уровней. Эмпирическая схема уровней атома натрия изображена на рис. 200. Схемы уровней других щелочных металлов имеют такой же характер, как у натрия.

Схема уровней натрия (рис. 200) отличается от схемы уровней водородного атома (рис. 198) тем, что аналогичные уровни в различных рядах лежат на неодинаковой высоте. Несмотря на это отличие, обе схемы обнаруживают большое сходство. Это сходство дает основание предположить, что спектры щелочных металлов испускаются при переходах самого внешнего (так называемого валентного или опти ческого) электрона с одного уровня на другой.

Из рис. 200 видно, что энергия состояния оказывается зависящей, кроме числа п, также от того, в какой ряд попадает данный терм, т. е. от номера ряда термов. На схеме уровней атома водорода различные ряды термов (с совпадающими по высоте уровнями) отличаются значениями момента импульса электрона. Естественно предположить, что различные ряды термов щелочных металлов также отличаются значениями момента импульса оптического электрона. Поскольку уровни различных рядов в этом случае не лежат на одинаковой высоте, следует принять, что энергия оптического электрона в атоме щелочного металла зависит от величины момента импульса электрона (чего мы не наблюдали для водорода).

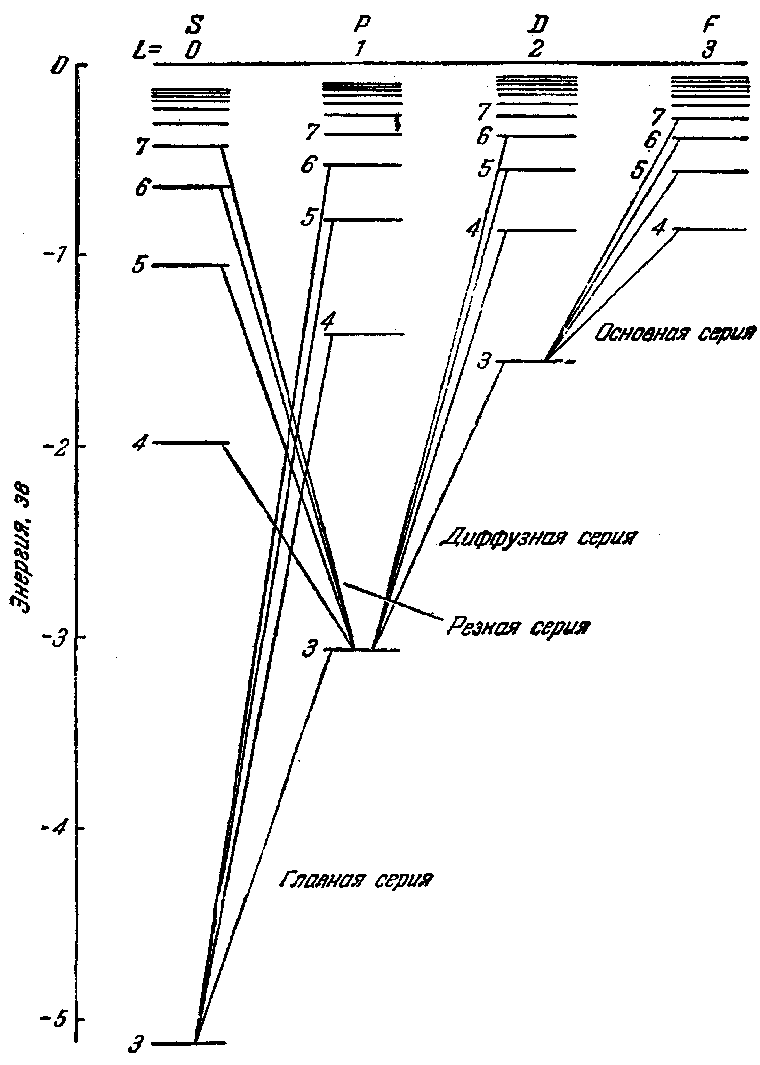
Рис. 200.

В более сложных, чем водород, атомах, имеющих несколько электронов, можно считать, что каждый из электронов движется в усредненном поле ядра и остальных электронов. Это™'поле уже не будет кулоновским (т. е. пропорциональным ), но обладает центральной симметрией (зависит только от г). В самом деле, в зависимости от степени проникновения электрона в глубь атома заряд ядра будет для данного электрона в большей или меньшей степени экранироваться другими электронами, так что эффективный заряд, воздействующий на рассматриваемый электрон, не будет постоянным. Вместе с тем, поскольку электроны движутся в атоме с огромными скоростями, усредненное по времени поле можно считать центрально-симметричным.

Решение уравнения Шредингера (65.3) для электрона, движущегося в центрально-симметричном некуло-новском поле, дает результат, аналогичный результату для водородного атома, с тем отличием, что энергетические уровни зависят не только от квантового числа п, но и от квантового числа l:

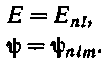
Таким образом, в этом случае снимается вырождение по /. Отличие в энергии между состояниями с различными / и одинаковыми п вообще не так велико, как между состояниями с различными п. С увеличением / энергия уровней с одинаковыми п возрастает.

Числа / и т по-прежцему определяют момент импульса электрона и его проекцию на заданное направление.

Момент импульса атома в целом слагается из моментов всех электронов, входящих в состав атома. Сложение моментов импульса осуществляется по квантовым "законам, согласно которым величина результирующего момента М определяется выражением:

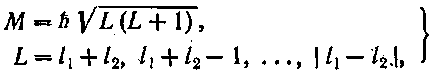(70.2)

(70.3)

где и —числа, определяющие складываемые моменты Mi и М₂ по формуле:

Таким образом, результирующий момент может иметь или (нужно взятъ меньшее из двух /) различных значений.

Исследования оптических спектров ионов щелочных металлов показали, что мЪмент импульса атомного остатка (т. е. ядра и остальных электронов, кроме наименее связанного 'оптического электрона, удаляющегося при ионизации) равен нулю. Следовательно, момент атома щелочного металла равен моменту его оптического электрона и L атома совпадает с / этого электрона.

Поскольку при возбуждении атома и испускании света остальные электроны не изменяют своего энергетического состояния, схему уровней атома можно считать тождественной схеме уровней оптического электрона. Таким образом, квантовая механика объясняет все особенности приведенной на рис. 200 схемы.

На рис. 200 показаны переходы между уровнями, приводящие к возникновению различных серий. Эти переходы подчиняются действующему и в данном случае правилу отбора: возможны лишь такие переходы, при которых момент атома изменяется на единицу:

Из всего сказанного выше становится ясным происхождение символови т. д. Будучи заимствованы из названий спектральных серий, эти буквы послужили вначале для обозначения рядов термов, а затем были перенесены на состояния с соответствующими значениями L или /.